
Of Symmetry, Cymatics, and Beauty: The Hexagon
I was sitting alone in a church, letting the stillness and silence filter in, when I felt the power that acoustics, beauty, and architecture have over individuals, and how they’ve always been intertwined. At the time I was visiting Europe, and my travels led me to a cathedral in Belgium. The art, blurred with its historical prevalence, marinated into an experience that changes the individual who walks through with eyes open.
I was attempting to understand the patterns, flow, and reasoning behind the architectural decisions and why they mattered. What kind of influence did architecture and sound and symmetry have on societies and communities, and how did beauty affect it all? While I did not have the answers, my research on this question suggested that nature did.
While at first a field that is seemingly unrelated to economics, there’s plenty of discussions to be had about how the natural economy and its effect on economics by analyzing the link between the two: mathematics. The natural world is full of patterns, as all of the science follows the natural code—what we know to be mathematics. Historical analysis and scientific hypothesis offer an explanation for how patterns and shapes affect culture, and why we have a strong proclivity to find efficient ways of organizing ourselves as a community—as laid out by the economic efficiency theory.
Geometry in Nature
 Geometry is imbued in nature because nature’s foundation is mathematics, as math is the root of all sciences (pun intended). Researchers have discovered many plant growth rates that all follow basic mathematical functions, like linear, log, power, and exponential functions—and have still to discover even more. Often these plants will follow symmetrical growth patterns, resulting in fascinating geometric patterns.
Geometry is imbued in nature because nature’s foundation is mathematics, as math is the root of all sciences (pun intended). Researchers have discovered many plant growth rates that all follow basic mathematical functions, like linear, log, power, and exponential functions—and have still to discover even more. Often these plants will follow symmetrical growth patterns, resulting in fascinating geometric patterns.
Geometry also takes place in sound; the harmonic series is an obvious demonstration of math’s connection to music; however, the most direct display of this is in the fascinating field of cymatics, or Chladi’s pitch, which is the discipline of studying visible sound and geometric shapes—a subset of modal phenomena that connects the two seemingly unrelated fields. While the underlying equations behind these geometric shapes are far more involved and complex, the observation of cymatics is quite simple; by simply rubbing a bow against a metal plate topped with sand, the patterns that result as a consequence of the modes of vibration were, and still are, astonishing. 
The Rosslyn Chapel demonstrates these fields as a perfect blend of mystery and scientific inquiry. Built in Scotland, the fifteenth-century church is located in the village of Roslin, which is located seven miles from Edinburgh. The Chapel has around 215 cubes where 13 geometric patterns are sequentially repeated.
 Using cymatics, father and son duo Tommy and Stuart Mitchell were able to decode a secret hymn, by matching each of the patterns on the carved cubes to a Chladni pitch. They discovered music sculpted into the architecture for hundreds of years, left in plain sight yet hidden in the beauty of the geometric shapes.
Using cymatics, father and son duo Tommy and Stuart Mitchell were able to decode a secret hymn, by matching each of the patterns on the carved cubes to a Chladni pitch. They discovered music sculpted into the architecture for hundreds of years, left in plain sight yet hidden in the beauty of the geometric shapes.
The Hexagon
We may observe nature’s little engineers, the bees and their famous honeycombs, as examples of why economizing space is so valuable. Bees forge their honeycombs out of wax, a material that they must fly 150,000 miles to yield one pound of beeswax (530,000 km/kg) This is roughly equivalent to a bee traveling six times around the Earth; it takes substantial energy and bee power to come up with just a pound of beeswax, which is used for vital functions such as storing food and raising larvae. It follows, then, that bees want to be as efficient as possible with the usage of their beeswax, as it’s an important and rare resource.
The honeycombs, therefore, result in hexagonal shapes because they are one of the most efficient geometrical shapes that can cover curved surfaces with minimal area wastage. Indeed, Earth and its layers—specifically the crust observes the same pattern of achieving efficiency, as demonstrated by phenomena like Giant’s Causeway.
The Giant’s Causeway is a coastline that stretches four miles long in Northern Ireland, and has been a source of myth and legend for centuries, as the shore is uniquely characterized by its 40,000 basalt hexagonal columns. Despite hexagons appearing frequently in the natural world, scientists first started to seriously consider nature as the motive behind the Giant’s Causeway in the late 18th century, when French scientist Nicolas Demarest discarded the hypothesis that humans had, in the past, created the rock formations; rather, he suggested volcanic activity to be the reason, which remains the accepted theory today. The columns are predominantly made of basalt, an extrusive volcanic rock that is commonly found at divergent plate boundaries on the mid-ocean ridge systems where volcanic activity happens frequently. The vast amount of basalt present suggests that there was an incredible amount of volcanic activity, which historically makes sense as these lava flows are associated with the spreading of the North American and European plates.
 Mass amounts of volcanic activity tend to form a’a, a stringy, ropey form of lava which both start as lava emerging from a vent. Lava volumetric flow rates vary in their cooling rate. Upon contact with the surface, lava will immediately begin to cool. At first, this cooling is extremely rapid, which causes a hardened crust to form on top of the lava, insulating the still liquid lava below. The insulated liquid elongates the cooling process, a process that could take up years for the thick lava to completely cool. As the lava dries out, cracks on the crust start to form in the now basalt rock. It is presumed that the cracks will move in such a way as to maximize the release rate of the elastic energy. Given this efficiency principle, hexagons are the best pattern to accomplish that. Like the honeybees, the very crust of the Earth is in tune with the natural code. The explanation behind nature’s tendency towards efficiency lies in the equation of the hexagon; the equation shows that hexagons tessellate a plane, meaning that the hexagon leaves no space when grouped around a corner. This is shown in the following proof:
Mass amounts of volcanic activity tend to form a’a, a stringy, ropey form of lava which both start as lava emerging from a vent. Lava volumetric flow rates vary in their cooling rate. Upon contact with the surface, lava will immediately begin to cool. At first, this cooling is extremely rapid, which causes a hardened crust to form on top of the lava, insulating the still liquid lava below. The insulated liquid elongates the cooling process, a process that could take up years for the thick lava to completely cool. As the lava dries out, cracks on the crust start to form in the now basalt rock. It is presumed that the cracks will move in such a way as to maximize the release rate of the elastic energy. Given this efficiency principle, hexagons are the best pattern to accomplish that. Like the honeybees, the very crust of the Earth is in tune with the natural code. The explanation behind nature’s tendency towards efficiency lies in the equation of the hexagon; the equation shows that hexagons tessellate a plane, meaning that the hexagon leaves no space when grouped around a corner. This is shown in the following proof:
 Mathematician Marcus Du Sautoy explained that there could have been three possible shapes the bees could have used that would not leave spaces between each shape, as circles and pentagons would. Those were equilateral triangles, squares, and hexagons. Triangles have been discovered to use the most beeswax, and white squares are a bit better at economizing space, Marcus Du Sautoy says that “the hexagonal array is the most efficient storage solution the bees could have chosen.” Charles Darwin described this phenomenon as “absolutely perfect in economizing labor and wax.” Despite the age of hexagons’ existence, Du Sautoy explained that “it’s a solution that was only mathematically proven a few years ago.” It took nearly four hundred years to prove an equation that nature has been operating on since its existence, and that was accomplished by mathematician Thomas Hales in 1998.
Mathematician Marcus Du Sautoy explained that there could have been three possible shapes the bees could have used that would not leave spaces between each shape, as circles and pentagons would. Those were equilateral triangles, squares, and hexagons. Triangles have been discovered to use the most beeswax, and white squares are a bit better at economizing space, Marcus Du Sautoy says that “the hexagonal array is the most efficient storage solution the bees could have chosen.” Charles Darwin described this phenomenon as “absolutely perfect in economizing labor and wax.” Despite the age of hexagons’ existence, Du Sautoy explained that “it’s a solution that was only mathematically proven a few years ago.” It took nearly four hundred years to prove an equation that nature has been operating on since its existence, and that was accomplished by mathematician Thomas Hales in 1998.
An Astronomical Mystery
Because of their economic efficiency, hexagons appear frequently in the ecosphere; turtle’s shells have hexagonal patterns, making their shells very durable and tough, and fruit flies have hexagonal shapes in their eyes, giving them the best ultra-vibrant eyesight known to the world. Hexagons also appear at the sub-atomic level, most notably seen in Graphene, an allotrope of carbon that is arranged in a hexagonal lattice, which also happens to be the strongest material ever discovered. Most striking, however, is the hexagon-shaped cloud on Saturn.

Figure 4 Saturn’s Hexagon
As of today, there only exist hypotheses about the cloud shape. It spans around 20,000 miles in length on the northernmost point on Saturn, which is roughly three times the size of the earth. Located in the center is the eye of the storm, approximately 50 times larger than an average hurricane storm on Earth, and has been around for possibly hundreds of years, compared to the average week-long life of hurricanes on Earth. There is no hexagon on the South pole, as verified by Cassini. Researchers have developed a model for the hexagon that describes the shape as resembling a stationary Rossby wave, which blows in an eastward direction on Saturn and is “pinched” by smaller, shallow storms, effectively warping the stream into a hexagon. Another theory suggests a similar model, but measures zonal jets to be thousands of miles deeper than the previous theory. One hypothesis that is particularly interesting is that cymactical frequencies are the causal factor of Saturn’s hexagon. John Stuart Reid, the creator of the CymaScope, created the following chart and theorizes that low-frequency sound energy disrupts the crust of Saturn, where high-speed winds create circular palisades that act as boundary conditions to the low-frequency event.
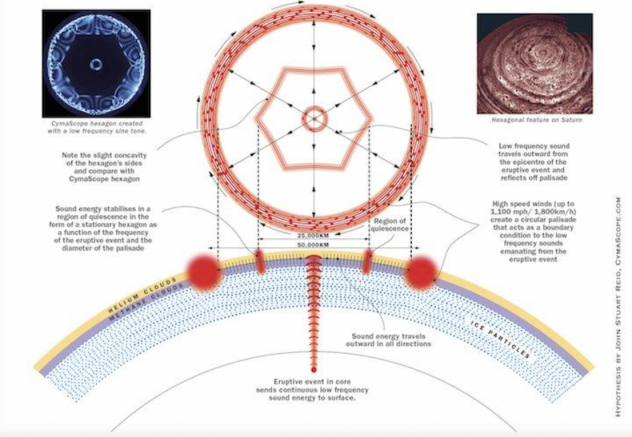 The connection between Saturn’s hexagon is more than just an efficient way of releasing pressure; it could very well be cymatics at work, a song for the universe. Because the basis behind nature’s economy is math, which is the same basis behind how we, as economists, analyze our economies, we therefore know that the same foundational background has spillover effects.
The connection between Saturn’s hexagon is more than just an efficient way of releasing pressure; it could very well be cymatics at work, a song for the universe. Because the basis behind nature’s economy is math, which is the same basis behind how we, as economists, analyze our economies, we therefore know that the same foundational background has spillover effects.
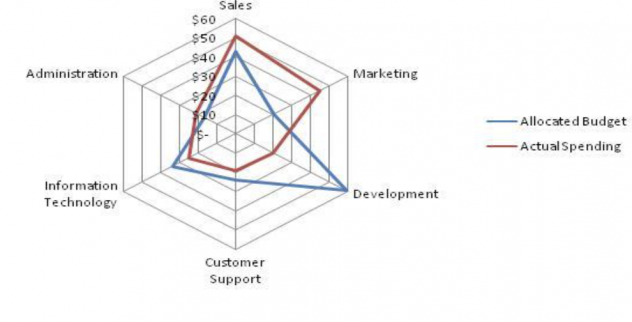 We see this in radar charts, (fig. 5) which display multivariable methods through numerous model systems. The Black-Scholes model originated from the heat equation, using partial differentials to relate the Black-Scholes differential equation to numerous variables. Irving Fisher, an American economist responsible for a fundamental relationship in economics that describes the relationship between nominal and real interest rates has origins in statical techniques and thermodynamics.
We see this in radar charts, (fig. 5) which display multivariable methods through numerous model systems. The Black-Scholes model originated from the heat equation, using partial differentials to relate the Black-Scholes differential equation to numerous variables. Irving Fisher, an American economist responsible for a fundamental relationship in economics that describes the relationship between nominal and real interest rates has origins in statical techniques and thermodynamics.
What the Hexagon Tells Us
By following the natural code, nature devises beautiful and complex-looking structures and systems, all the while maintaining efficiency.
Nature’s economy relies on a mathematical blueprint and structure; because economics shares the same blueprint; when we walk into cathedrals or other architectural structures that inspire us, behind the history and lore, there’s more to the aesthetics than meets the eye, and seeking out the mystery behind phenomena is what economics is all about.
Featured Image Source: Business Insider
Disclaimer: The views published in this journal are those of the individual authors or speakers and do not necessarily reflect the position or policy of Berkeley Economic Review staff, the Undergraduate Economics Association, the UC Berkeley Economics Department and faculty, or the University of California, Berkeley in general.

